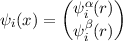
TURBOMOLE provides two different possibilities for the treatment of relativistic effects: Via effective core potentials (ECPs) or via all-electron approaches (X2C, DKH, BSS). Both techniques can be employed in an one-component (scalar relativistic) or two-component (including spin-orbit coupling) framework. The latter is only available in the module RIDFT.
Incoporation of scalar-relativistic effects leads to additional contributions to the one-electron integrals (either from ECP or all-electron approach). The program structure is the same as in non-relativistic theory( all quantities are real). Two-component treatments allow for self-consistent calculations including spin-orbit interactions. These may be particularly important for compounds containing heavy elements (additionally to scalar relativistic effects). Two-component treatments require the use of complex two-component orbitals
|
|
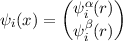instead of real (non-complex) one-component orbitals needed for non-relativistic or scalar-relativistic treatments. The Hartree-Fock and Kohn-Sham equations are now spinor equations with a complex Fock operator
 |
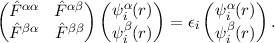The wavefunction is no longer eigenfunction of the spin operator, the spin vector is no longer an observable.
In case of DFT for open-shell systems rotational invariance of the exchange-correlation energy
was ensured by the non-collinear approach. In this approach the exchange-correlation
energy is a functional of the particle density and the absolute value of the spin-vector
density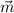 
(r) (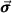
are the Pauli matrices)
 |
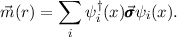This quantity replaces the spin-density (difference between density of alpha and beta electrons) of non- or scalar-relativistic treatments.
For closed-shell species the Kramers-restricted scheme, a generalization of the RHF-scheme of one component treatments, is applicable.
Effective core potentials The most economic way to account for relativistic effects is via effective core potentials by choosing either the one- or the two-component ECP (and for the latter additionally setting $soghf in the control file). The theoretical background and the implementation for the two-component SCF procedure is described in [90]. The backgrund theory of the more fundamental approach, all-electron relativistic electronic structure theory, is given in the next paragraph.
Relativistic all-electron approaches (X2C, DKH, BSS) Relativistic calculations are based on the Dirac rather than on the Schrödinger Hamiltonian. Since the Dirac Hamiltonian introduces pathological negative-energy states and requires extensive one-electron basis set expansions, methods have been devised which allow one to calculate a matrix representation of that part of the Dirac Hamiltonian, which describes electronic states only. For this, a unitary transformation is employed to block-diagonalize the Dirac Hamiltonian and thus to decouple the negative-energy from the electronic states. In order to be efficient, this transformation is carried out only for the one-electron part of the full Hamiltonian (as a consequence, the two-electron interaction will then be affected by a picture-change effect). The resulting quantum chemical approach has been called an exact two-component (X2C) one. It was developed by many groups starting with formal work in the mid 1980s. X2C is related to the step-wise Douglas-Kroll-Hess (DKH) approach, which also achieves exact decoupling but sequentially. The number of transformation steps is called the order of DKH. X2C is also related to the Barysz-Sadlej-Snijders (BSS) method, that first applies the free-particle Foldy-Wouthuysen transformation (which is the first mandatory step in DKH), and then constructs the one-step exact decoupling transformation of X2C. These three approaches have been reviewed and directly compared in terms of formalism and results, respectively, in Ref. [91] (see also this reference for a complete bibliography on exact-decoupling methods).
Essentially, X2C methods change the one-electron Hamiltonian in basis-set representation. The Schrödinger one-electron Hamiltonian (including the external potential of the atomic nuclei) is replaced by the transformed (upper-left block of the) Dirac Hamiltonian. Since the transformation is carried out in the fully decontracted primitive basis, all matrix operations needed for the generation of the relativistic one-electron Hamiltonian can be cumbersome and even prohibitive if the size of the molecule is large. In order to solve this unfavorable scaling problem, a rigorous local approach, called DLU, has been devised [92] and should be activated for large molecules. However, since the local (atomic) structure is defined by the atom-centered basis functions within DLU, diffuse functions in the basis set should be handled with care and the use of tailored basis sets is recommended (relativistic calculations require refitted basis sets; if these are not available for X2C or X2C-DLU, standard second-order DKH basis sets could be used).
As in DKH theory, X2C and BSS exist in full two-component (spin-(same-)orbit coupling including) and in a one-component scalar relativistic form. Both have been implemented into the TURBOMOLE package and all details on the efficient implementation have been described in Ref. [93], which should be cited when the module is activated.
The keyword $soghf enforces the two-component calculations. Keywords for specification of the method of calculation are the same as for the one-component case.
The DIIS scheme for complex Fock operators can be activated by inserting $gdiis in the control-file. For closed-shell species a Kramers invariant density functional formalism (only pure density functionals) can be switched on with the keyword $kramers. These keywords have to be inserted into the control-file manually.
As start wavefunctions Hückel-, UHF- or RHF-wavefunctions may be used. The two-component formalism supports Abelian point group symmetry if $kramers is set. Otherwise start wave functions may be transformed to C1 symmetry by define or the script ’uhfuse’. For open-shell molecules it is often helpful to increase the value for $scforbitalshift closedshell; a value of ca. 1.0 may serve as a rough recommendation.
Effective core potentials The two-component formalism may be most easily prepared and applied in the following way:
All-electron calculations The keywords $rx2c, $rbss and $rdkh [Order of DKH] are used to activate the X2C, BSS or DKH Hamiltonian. The default order of the DKH Hamiltonian is four. It is not recommended to go beyond, but to use X2C instead. For details on the arbitrary-order DKH Hamiltonians see Ref. [95] for details on the infinite-order DKH theory, [96] for the implementation, and [97] for a conceptual review of DKH theory. The local approach (DLU) can be optionally activated by $rlocal for all one- and two-component all-electron Hamiltonians. For symmetric molecules, point-group symmetry is not exploited by default, but can be used in the one-component case by setting $rsym.