1.3 How to Quote Usage of TURBOMOLE
Please quote the usage of the program package under consideration of the version
number:
|
| TURBOMOLE V7.2 2017, a development of University of Karlsruhe and |
| Forschungszentrum Karlsruhe GmbH, 1989-2007, |
| TURBOMOLE GmbH, since 2007; available from |
| http://www.turbomole.com. |
|
| |
A LaTeX template could look like this:
@misc{TURBOMOLE,
title = {{TURBOMOLE V7.2 2017}, a development of {University of Karlsruhe} and
{Forschungszentrum Karlsruhe GmbH}, 1989-2007,
{TURBOMOLE GmbH}, since 2007; available from \\
{\tt http://www.turbomole.com}.}}
Scientific publications require proper citation of methods and procedures employed. The
output headers of TURBOMOLE modules include the relevant papers. One may also use the
following connections between: method [module] number in the subsequent list (For
module ricc2 see also Section 10).
- Programs and methods
- general program structure and features: I
- HF-SCF [dscf, ridft]: II
- DFT (quadrature) [dscf, ridft, escf, aoforce]: IV, d (m grids)
- RI-DFT [ridft, aoforce, escf, riper]: c, d, XXIII (marij), VII
(escf), XXIV (aoforce)
- periodic DFT [riper]: XXXIX, XLI, XLII, XL
- MP2 [mpgrad]: III
- RI-MP2 [ricc2]: energies and gradients VIII, XXIX, f, and (static)
polarizabilities XXXVI
- PNO-MP2 [pnoccsd]: energies XXXVII
- stability analysis [escf]: V
- electronic excitations with CIS, RPA, TD-DFT
[escf]: VI, VII, XVIII, XXVII
- excited state structures and properties with CIS, RPA, TD-DFT
[egrad]: XIX, XXVI, XXVII
- RI-CC2 [ricc2]:
- singlet XII and triplet excitation energies XIII
- transition moments and first-order properties of excited states XV
and first-order properties for triplet states XIV
- ground state geometry optimizations XXI
- excited state geometry optimizations and relaxed properties XXII
- parallelization XXIX
- spin-component scaled (SCS) variants XXXII
- frequency-dependent and static polarizabilities XXXVI
- RI-ADC(2), RI-CIS(D) and RI-CIS(D∞) [ricc2]: XXVIII
- SOS variants of MP2, CIS(D), CIS(D∞), ADC(2) and CC2 with
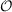 (
(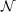 4)-scaling
XXXIII
4)-scaling
XXXIII
- analytical second derivatives (force fields) [aoforce]: XVI, XVII
- RI-JK [ridft]: XX
- NMR chemical shifts [mpshift]: IX (MP2)
- parallel DFT [ridft]: X
- geometry optimization in redundant internal coordinates [relax]: XI
- RI integral evaluation: XXV
- explicitly correlated F12 methods for ground state energies [ccsdf12and
pnoccsd]: MP2-F12 XXXIV, PNO-MP2-F12 XXXVIII, MP3-F12 XXXV,
MP4(F12*) XXXV, CCSD(F12) XXXI, CCSD(F12*) XXXV, CCSD(F12)(T)
XXXI, CCSD(F12*)(T) XXXV
- Local hybrid calculations: XLIII ([ridft]), XLIV ([grad,rdgrad]), XLV
([escf])
- Orbital and auxiliary basis sets
- basis sets:
- SV, SV(P), SVP, DZ (a), TZV, TZVP, TZVPP (b), TZVPP(Rb-Hg)
(f), QZV, QZVP, QZVPP (i)
- new balanced basis sets (with smaller ECPs, i.e. the def2 basis sets): j
- all-electron basis sets for Rb to Xe (SVPall, SVPPall, TZVPall,
TZVPPall): g
- references for the correlation consistent basis sets (cc-pVXZ, etc.) can
be found e.g. at
http://tyr0.chem.wsu.edu/ kipeters/Pages/cc_append.html
or http://www.emsl.pnl.gov/forms/basisform.html.
kipeters/Pages/cc_append.html
or http://www.emsl.pnl.gov/forms/basisform.html.
Note, that most of the correlation consistent basis sets in the basis set
library of TURBOMOLE have been downloaded from the latter EMSL
web site and therefore users are requested to include in addition to
the original scientific reference an appropriate citation (see web site)
in any publications resulting from the use of these basis sets.
- property–optimized augmentations: def2-SVPD, def2-TZVPD,
def2-TZVPPD, def2-QZVPD,def2-QZVPPD (n).
- basis sets for Dirac–Fock ECPs, i.e. the dhf basis sets: o.
- auxiliary basis sets for RI-DFT: c, d, e
- auxiliary basis sets for RI-MP2: f, k, h (for Dunning basis sets)
Further references of papers not from the TURBOMOLE group are given in the bibliography.
The following publications describe details of the methodology implemented in
TURBOMOLE:
Methods
-
I.
- Electronic Structure Calculations on Workstation Computers: The Program
System TURBOMOLE. R. Ahlrichs, M. Bär, M. Häser, H. Horn and
C. Kölmel; Chem. Phys. Letters 162, 165 (1989).
-
II.
- Improvements on the Direct SCF Method. M. Häser and R. Ahlrichs;
J. Comput. Chem. 10, 104 (1989).
-
III.
- Semi-direct MP2 Gradient Evaluation on Workstation Computers: The
MPGRAD Program. F. Haase and R. Ahlrichs; J. Comp. Chem. 14, 907
(1993).
-
IV.
- Efficient Molecular Numerical Integration Schemes.
O. Treutler and R. Ahlrichs; J. Chem. Phys. 102, 346 (1995).
-
V.
- Stability Analysis for Solutions of the Closed Shell Kohn–Sham Equation.
R. Bauernschmitt and R. Ahlrichs; J. Chem. Phys. 104, 9047 (1996).
-
VI.
- Treatment of Electronic Excitations within the Adiabatic Approximation of
Time Dependent Density Functional Theory.
R. Bauernschmitt and R. Ahlrichs; Chem. Phys. Letters 256, 454 (1996).
-
VII.
- Calculation of excitation energies within time-dependent density functional
theory using auxiliary basis set expansions. R. Bauernschmitt, M. Häser,
O. Treutler and R. Ahlrichs; Chem. Phys. Letters 264, 573 (1997).
-
VIII.
- RI-MP2: first derivatives and global consistency. F. Weigend and M. Häser;
Theor. Chem. Acc. 97, 331 (1997).
-
IX.
- A direct implementation of the GIAO-MBPT(2) method for calculating NMR
chemical shifts. Application to the naphthalenium and anthracenium ions.
M. Kollwitz and J. Gauss; Chem. Phys. Letters 260, 639 (1996).
-
X.
- Parallelization of Density Functional and RI-Coulomb Approximation in
TURBOMOLE. M. v. Arnim and R. Ahlrichs; J. Comp. Chem. 19, 1746
(1998).
-
XI.
- Geometry optimization in generalized natural internal Coordinates.
M. v. Arnim and R. Ahlrichs; J. Chem. Phys. 111, 9183 (1999).
-
XII.
- CC2 excitation energy calculations on large molecules using the resolution of
the identity approximation. C. Hättig and F. Weigend; J. Chem. Phys. 113,
5154 (2000).
-
XIII.
- Implementation of RI-CC2 for triplet excitation energies with an application to
trans-azobenzene. C. Hättig and Kasper Hald; Phys. Chem. Chem. Phys. 4
2111 (2002).
-
XIV.
- First-order properties for triplet excited states in the approximated Coupled
Cluster model CC2 using an explicitly spin coupled basis. C. Hättig, A. Köhn
and Kasper Hald; J. Chem. Phys. 116, 5401 (2002) and Vir. J. Nano. Sci.
Tech., 5 (2002).
-
XV.
- Transition moments and excited-state first-order properties in the
coupled-cluster model CC2 using the resolution-of-the-identity approximation.
C. Hättig and A. Köhn; J. Chem. Phys. 117, 6939 (2002).
-
XVI.
- An efficient implementation
of second analytical derivatives for density functional methods. P. Deglmann,
F. Furche and R. Ahlrichs; Chem. Phys. Letters 362, 511 (2002).
-
XVII.
- Efficient characterization of stationary points on potential energy surfaces.
P. Deglmann and F. Furche; J. Chem. Phys. 117, 9535 (2002).
-
XVIII.
- An improved method for density functional calculations of the
frequency-dependent optical rotation.
S. Grimme, F. Furche and R. Ahlrichs; Chem. Phys. Letters 361,321 (2002).
-
XIX.
- Adiabatic time-dependent density functional methods for excited state
properties. F. Furche and R. Ahlrichs; J. Chem. Phys. 117, 7433 (2002),
J. Chem. Phys. 121, 12772 (2004) (E).
-
XX.
- A fully direct RI-HF algorithm:
Implementation, optimised auxiliary basis sets, demonstration of accuracy and
efficiency. F. Weigend, Phys. Chem. Chem. Phys. 4, 4285 (2002)
-
XXI.
- Geometry optimizations with the coupled-cluster model CC2 using the
resolution-of-the-identity approximation. C. Hättig; J. Chem. Phys. 118,
7751, (2003).
-
XXII.
- Analytic gradients for excited states in the coupled-cluster model CC2
employing the resolution-of-the-identity approximation. A. Köhn and C. Hättig;
J. Chem. Phys., 119, 5021, (2003).
-
XXIII.
- Fast evaluation of the Coulomb potential for electron densities using multipole
accelerated resolution of identity approximation. M. Sierka, A. Hogekamp and
R. Ahlrichs;J. Chem. Phys. 118, 9136, (2003).
-
XXIV.
- Nuclear
second analytical derivative calculations using auxiliary basis set expansion.
P. Deglmann, K. May, F. Furche and R. Ahlrichs; Chem. Phys. Letters 384,
103, (2004).
-
XXV.
- Efficient evaluation of three-center two-electron integrals over Gaussian
functions. R. Ahlrichs; Phys. Chem. Chem. Phys. 6, 5119, (2004).
-
XXVI.
- Analytical time-dependent density functional derivative methods within the
RI-J approximation, an approach to excited states of large molecules. D.
Rappoport and F. Furche, J. Chem. Phys. 122, 064105 (2005).
-
XXVII.
- Density functional theory for excited states: equilibrium structure and
electronic spectra. F. Furche and D. Rappoport, Ch. III of "Computational
Photochemistry", Ed. by M. Olivucci, Vol. 16 of "Computational and
Theoretical Chemistry", Elsevier, Amsterdam, 2005.
-
XXVIII.
- Structure optimizations for excited states with correlated second-order
methods: CC2, CIS(D∞), and ADC(2). Christof Hättig, Adv. Quant. Chem.,
50, 37-60 (2005).
-
XXIX.
- Distributed memory parallel implementation of
energies and gradients for second-order Møller-Plesset perturbation theory with
the resolution-of-the-identity approximation. Christof Hättig, Arnim Hellweg,
Andreas Köhn, Phys. Chem. Chem. Phys. 8, 1159-1169, (2006).
-
XXX.
- Self-consistent treatment of spin-orbit interactions with efficient Hartree-Fock
and density functional methods. Markus K. Armbruster, Florian Weigend,
Christoph van Wüllen, Wim Klopper, Phys. Chem. Chem. Phys. 10, 1748 -
1756, (2008).
-
XXXI.
- Quintuple-ζ quality coupled-cluster correlation energies with triple-ζ basis sets.
David P. Tew, Wim Klopper, Christian Neiss, Christof Hättig, Phys. Chem.
Chem. Phys. 9 921–1930 (2007).
-
XXXII.
- Benchmarking the performance of spin-component scaled CC2 in ground and
electronically excited states. Arnim Hellweg, Sarah A. Grün, Christof Hättig,
Phys. Chem. Chem. Phys., 10, 4119-4127 (2008).
-
XXXIII.
- Scaled opposite-spin CC2 for ground and excited states with fourth order scaling
computational costs. Nina O. C. Winter, Christof Hättig, J. Chem. Phys., 134,
184101 (2011).
and: Quartic scaling analytical gradients of scaled opposite-spin CC2. Nina O.
C. Winter, Christof Hättig, Chem. Phys. 401 (2012) 217.
-
XXXIV.
- The MP2-F12 Method in the TURBOMOLE Programm Package. Rafal A.
Bachorz, Florian A. Bischoff, Andreas Glöß, Christof Hättig, Sebastian Höfener,
Wim Klopper, David P. Tew, J. Comput. Chem. 32, 2492–2513 (2011).
-
XXXV.
- Accurate and efficient approximations to explicitly correlated coupled-cluster
singles and doubles, CCSD-F12. Christof Hättig, David P. Tew, Andreas Köhn,
J. Chem. Phys. 132, 231102 (2010).
-
XXXVI.
- Large scale polarizability calculations using the approximate coupled
cluster model CC2 and MP2 combined with the resolution-of-the identity
approximation. Daniel H. Friese, Nina O. C. Winter, Patrick Balzerowski,
Raffael Schwan, Christof Hättig, J. Chem. Phys., 136, 174106 (2012).
-
XXXVII.
- A
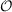 (
(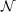 3)-scaling PNO-MP2 method using a hybrid OSV-PNO approach with
an iterative direct generation of OSVs. Gunnar Schmitz, Benjamin Helmich,
Christof Hättig, Mol. Phys. 111, 2463–2476, (2013).
3)-scaling PNO-MP2 method using a hybrid OSV-PNO approach with
an iterative direct generation of OSVs. Gunnar Schmitz, Benjamin Helmich,
Christof Hättig, Mol. Phys. 111, 2463–2476, (2013).
-
XXXVIII.
- Explicitly correlated PNO-MP2 and PNO-CCSD and its application to the S66
set and large molecular systems. Gunnar Schmitz, Christof Hättig, David Tew,
Phys. Chem. Chem. Phys. 16, 22167–22178 (2014).
-
XXXIX.
- Density functional theory for molecular and periodic systems using density
fitting and continuous fast multipole methods. Roman Łazarski, Asbjörn M.
Burow, Marek Sierka, J. Chem. Theory Comput. 11, 3029–3041 (2015).
-
XL.
- Low-memory iterative density fitting. Lukáš Grajciar, J. Comput. Chem. 36,
1521–1535 (2015).
-
XLI.
- Linear scaling hierarchical integration scheme for the exchange-correlation term
in molecular and periodic systems. A. M. Burow, M. Sierka, J. Chem. Theory
Comput. 7, 3097–3104 (2011).
-
XLII.
- Resolution of identity approximation for the Coulomb term in molecular and
periodic systems. A. M. Burow, M. Sierka, F. Mohamed, J. Chem. Phys. 131,
214101 (2009).
-
XLIII.
- Efficient self-consistent implementation of local hybrid functionals. H.
Bahmann, M. Kaupp, J. Chem. Theory Comput., 11, 1540–1548, (2015).
-
XLIV.
- Implementation of molecular gradients for local hybrid density functionals using
seminumerical integration techniques. S. Klawohn, H. Bahmann, M. Kaupp, J.
Chem. Theory Comput. 12, 4254–4262, (2016).
-
XLV.
- Efficient semi-numerical implementation of global and local hybrid functionals
for time-dependent density functional theory. T. M. Maier, H. Bahmann, M.
Kaupp, J. Chem. Theory Comput. 11, 4226–4237, (2015).
Basis sets
The following tables can be used to find the proper citations of the standard orbital and
auxiliary basis sets in the TURBOMOLE basis set library.
Orbital basis sets, elements H–Kr
Note: For H–Kr def-SV(P), def-SVP, ... are identical with the basis sets without def prefix. def2-QZVPP
and def2-QZVP are identical with QZVPP and QZVP.
def2-XVPD/XVPPD denotes the property–optimized augmentations def2-SVPD,
def2-TZVPD, def2- TZVPPD, def2-QZVPD,def2-QZVPPD.
Orbital basis sets, elements Rb–Rn
|
|
|
|
|
|
|
|
|
| | Rb | Sr | Y–Cd | In–Cs | Ba | La–Hg | Tl–At | Rn |
|
|
|
|
|
|
|
|
|
| def-SVP,def-SV(P),def-TZVP | d | d | d | d | d | d | d | j |
|
|
|
|
|
|
|
|
|
| def-TZVPP | f | d | f | f | d | f | d | j |
|
|
|
|
|
|
|
|
|
| def2-SV(P) | j | d | d | j | d | d | j | j |
|
|
|
|
|
|
|
|
|
| def2-SVP | j | d | j | j | d | j | j | j |
|
|
|
|
|
|
|
|
|
| def2-TZVP,def2-TZVPP |
|
|
|
|
|
|
|
|
|
|
| def2-QZVP,def2-QZVP |
|
|
|
|
|
|
|
|
|
|
| def2-XVPD/XVPPD, X=S,T,Q |
|
|
|
|
|
|
|
|
|
|
| |
Auxiliary basis sets for RI-DFT (Coulomb fitting)
|
|
|
|
| | H–Kr | Rb–At | Rn |
|
|
|
|
| (def-)SVP,(def-)SV(P) | c | d | l |
|
|
|
|
| (def-)TZVP | d | d | l |
|
|
|
|
| def2 universal | |
|
|
|
|
| |
Auxiliary basis sets for RI-MP2 and RI-CC, elements H–Ar
|
|
|
|
|
|
|
|
|
|
| | H | He | Li | Be | B–F | Ne | Na,Mg | Al–Cl | Ar |
|
|
|
|
|
|
|
|
|
|
| SVP,SV(P) | f | k | f | f | f | k | f | f | k |
|
|
|
|
|
|
|
|
|
|
| TZVP,TZVPP | f | k | f | f | f | k | f | f | k |
|
|
|
|
|
|
|
|
|
|
| QZVP,QZVPP |
|
|
|
|
|
|
|
|
|
|
|
| def2-SV(P) | f | k | m | f | f | k | m | f | k |
|
|
|
|
|
|
|
|
|
|
| def2-SVP | f | k | m | f | f | k | m | f | k |
|
|
|
|
|
|
|
|
|
|
| def2-TZVP,def2-TZVPP | f | k | f | m | f | k | m | m | k |
|
|
|
|
|
|
|
|
|
|
| def2-XVPD/XVPPD, X=S,T,Q |
|
|
|
|
|
|
|
|
|
|
|
| (aug-)cc-pVXZ, X=D–Q | h | h | k | k | h | h | k | h | h |
|
|
|
|
|
|
|
|
|
|
| (aug-)cc-pV5Z | k | k | - | - | k | k | - | k | k |
|
|
|
|
|
|
|
|
|
|
| cc-pwCVXZ, X=D–5 | - | - | - | - | k | k | - | k | k |
|
|
|
|
|
|
|
|
|
|
| |
Note: the auxiliary basis sets for the (aug-)cc-pV(X+d)Z basis sets for Al–Ar are identical with the
(aug-)cc-pVXZ auxiliary basis sets.
Auxiliary basis sets for RI-MP2 and RI-CC, elements K–Kr
|
|
|
|
|
|
| | K | Ca | Sc–Zn | Ga–Br | Kr |
|
|
|
|
|
|
| SVP,SV(P) | f | f | f | f | k |
|
|
|
|
|
|
| TZVP,TZVPP | f | f | f | f | k |
|
|
|
|
|
|
| QZVP,QZVPP |
|
|
|
|
|
|
|
| def2-SV(P) | m | f | f | f | k |
|
|
|
|
|
|
| def2-SVP | m | f | m | f | k |
|
|
|
|
|
|
| def2-TZVP,def2-TZVPP | m | f | m | f | k |
|
|
|
|
|
|
| def2-XVPD/XVPPD, X=S,T,Q |
|
|
|
|
|
|
|
| (aug-)cc-pVXZ, X=D–Q | - | - | - | h | h |
|
|
|
|
|
|
| (aug-)cc-pV5Z | - | - | - | p | p |
|
|
|
|
|
|
| cc-pCWVXZ, X=D–5 | - | - | - | p | p |
|
|
|
|
|
|
| (aug-)cc-pVXZ-PP, X=D–5 | - | - | - | p | p |
|
|
|
|
|
|
| cc-pwCVXZ-PP, X=D–5 | - | - | - | p | p |
|
|
|
|
|
|
| |
Auxiliary basis sets for RI-MP2 and RI-CC, elements Rb–Rn
|
|
|
|
|
|
|
|
|
|
| | Rb | Sr | Y–Cd | In–Xe | Cs | Ba | La–Hg | Tl–At | Rn |
|
|
|
|
|
|
|
|
|
|
| def-SVP,def-SV(P) | | m |
|
|
|
|
|
|
|
|
|
|
| def2-SVP,def2-SV(P) | m | f | f | m | m | f | f | m | m |
|
|
|
|
|
|
|
|
|
|
| def-TZVP,def-TZVPP | | m |
|
|
|
|
|
|
|
|
|
|
| def2-TZVP,def2-TZVPP |
|
|
|
|
|
|
|
|
|
|
|
| def2-QZVP,def2-QZVP |
|
|
|
|
|
|
|
|
|
|
|
| def2-XVPD/XVPPD, X=S,T,Q |
|
|
|
|
|
|
|
|
|
|
|
| aug-cc-pVXZ-PP, X=D–5 | - | - | - | p | - | - | - | p | p |
|
|
|
|
|
|
|
|
|
|
| cc-pwCVXZ-PP, X=D–5 | - | - | - | p | - | - | - | p | p |
|
|
|
|
|
|
|
|
|
|
| |
-
a.
- Fully Optimized Contracted Gaussian Basis Sets for Atoms Li to Kr. A. Schäfer,
H. Horn and R. Ahlrichs; J. Chem. Phys. 97, 2571 (1992).
-
b.
- Fully Optimized Contracted Gaussian Basis Sets of Triple Zeta Valence Quality for
Atoms Li to Kr. A. Schäfer, C. Huber and R. Ahlrichs; J. Chem. Phys. 100,
5829 (1994).
-
c.
- Auxiliary Basis Sets to Approximate Coulomb Potentials. K. Eichkorn,
O. Treutler, H. Öhm, M. Häser and R. Ahlrichs; Chem. Phys. Letters 242, 652
(1995).
-
d.
- Auxiliary basis sets for main row atoms and transition metals and their use to
approximate Coulomb potentials. K. Eichkorn, F. Weigend, O. Treutler and
R. Ahlrichs; Theor. Chem. Acc. 97, 119 (1997).
-
e.
- Accurate Coulomb-fitting basis sets for H to Rn. F. Weigend; Phys. Chem.
Chem. Phys. 8, 1057 (2006).
-
f.
- RI-MP2: Optimized Auxiliary Basis Sets and Demonstration of Efficiency. F.
Weigend, M. Häser, H. Patzelt and R. Ahlrichs; Chem. Phys. Letters 294, 143
(1998).
-
g.
- Contracted all-electron Gaussian basis sets for Rb to Xe. R. Ahlrichs and K. May;
Phys. Chem. Chem. Phys., 2, 943 (2000).
-
h.
- Efficient use of the correlation consistent basis sets in resolution of the identity
MP2 calculations. F. Weigend, A. Köhn and C. Hättig; J. Chem. Phys. 116,
3175 (2002).
-
i.
- Gaussian basis sets of quadruple zeta valence quality for atoms H–Kr. F. Weigend,
F. Furche and R. Ahlrichs; J. Chem. Phys. 119, 12753 (2003).
-
j.
- Balanced basis sets of split valence, triple zeta valence and quadruple zeta
valence quality for H to Rn: Design an assessment of accuracy. F. Weigend and
R. Ahlrichs; Phys. Chem. Chem. Phys. 7, 3297 (2005).
-
k.
- Optimization of auxiliary basis sets for RI-MP2 and RI-CC2 calculation:
Core-valence and quintuple-ζ basis sets for H to Ar and QZVPP basis sets for Li
to Kr. C. Hättig; Phys. Chem. Chem. Phys. 7, 59 (2005).
-
l.
- Accurate Coulomb-fitting basis sets for H to Rn. F. Weigend; Phys. Chem.
Chem. Phys. 8, 1057 (2006).
-
m.
- Optimized accurate auxiliary basis sets for RI-MP2 and RI-CC2 calculations
for the atoms Rb to Rn. A. Hellweg, C. Hättig, S. Höfener and W. Klopper;
Theor. Chem. Acc. 117, 587 (2007).
-
n.
- Property–optimized Gaussian basis sets for molecular response calculations. D.
Rappoport and F. Furche; J. Chem. Phys. 133, 134105 (2010).
-
o.
- Segmented contracted basis sets for one– and two–component Dirac–Fock effective
core potentials. F. Weigend and A. Baldes; J. Chem. Phys. 133, 174102 (2010).
-
p.
- Auxiliary basis sets for density-fitted correlated wavefunction calculations:
Weighted core-valence and ECP basis sets for post-d elements. C. Hättig,
G. Schmitz, J. Koßmann; Phys. Chem. Chem. Phys. 14, 6549 (2012).
-
q.
- Development of new auxiliary basis functions of the Karlsruhe segmented
contracted basis sets including diffuse basis functions (def2-SVPD, def2-TZVPPD,
and def2-QVPPD) for RI-MP2 and RI-CC calculations. A. Hellweg and D.
Rappoport; Phys. Chem. Chem. Phys. 17, 1010 (2015).
-
r.
- unpublished.
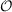 (
(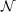 4)-scaling
XXXIII
4)-scaling
XXXIII
 kipeters/Pages/cc_append.html
or http://www.emsl.pnl.gov/forms/basisform.html.
kipeters/Pages/cc_append.html
or http://www.emsl.pnl.gov/forms/basisform.html.