9.2 Some Theory

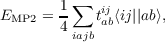
Second-order Møller–Plesset Perturbation Theory (MP2) corrects errors introduced by the mean-field ansatz of the Hartree–Fock (HF) theory. The perturbation operator is the difference the full electronic Hamiltonian and the Fock operator for occupied/occupied and virtual/virtual block. The MP2 energy is (in spin orbitals) given by:

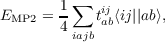(9.1)

with the doubles amplitudes

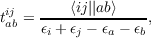(9.2)

i and j denote occupied, a and b virtual orbitals, ϵ_p are the corresponding orbital energies, and ⟨ij||ab⟩ = ⟨ij|ab⟩-⟨ij|ba⟩ are four-center two-electron repulsion integrals.

MP2 gradients (necessary for optimisation of structure parameters) are calculated as analytical derivatives of the MP2 energy with respect to nuclear coordinates. Calulation of these derivatives also yields the first order perturbed wave function, expressed as “MP2 density matrix”, in analogy to the HF density matrix. MP2 corrections to first-order properties like electric moments or atomic populations are obtained from the density matrix in the same way as for Hartree-Fock.

The “resolution of the identity (RI) approximation” means expansion of products of virtual and occupied orbitals in a basis of auxiliary functions. The calculation and transformation of the four-center two-electron integrals (see above) is replaced by that of three-center integrals, which leads to computational savings of RI-MP2 compared to a conventional MP2 calculations by a factor of ca. 5 (small basis sets like SVP) to ca. 10 (large basis sets like TZVPP) and more (for quadruple-ζ and larger basis sets). The RI errors—i.e. the errors due to the RI approximation—are with optimised auxliliary basis sets small and well documented [131,132]. The use of the mpgrad program is therefore only recommended for reference calculations or if suitable auxiliary basis sets are not available.

The OSV-PNO-MP2 implementation in the pnoccsd program is meant for large systems with ≿ 100 atoms where the costs for RI-MP2 calculations become unreasonable large. The OSV-PNO-MP2 implementation uses four additional approximations to reduce the scaling of the computational costs with the system size to about 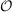(³):

• The truncation of the pair natural orbital (PNO) basis, ϕ_aij = ∑ _aϕ_ad_aa^ij for each pair ij of occupied orbitals to PNOs with occupation numbers n_a^ij ≥ T_PNO:

  ∑ bDabijd bbij = n bijd abij

  (9.3)

• The truncation of the orbital specific virtual (OSV) basis, ϕ_ãi = ∑ _aϕ_ad_aãⁱ for each occupied orbital i to OSVs with occupation numbers n_ãⁱ ≥ T_OSV:

  ∑ bDabiid bi = nid ai

  (9.4)

  The OSV basis is used to expand the PNOs. For a pair ij the PNOs are expanded in the union of the OSVs for the occupied orbitals i and j.
• The distant pair approximation: only such pairs ij are included in the correlation treatment for which the contribution to the correlation energy is expected (based on initially computed estimates) to be ≥ T_pair.
• The local RI approximation: two-electron integrals for a pair ij are expanded in a pair-specific subset of the full auxiliary basis which is determined based on an overlap criterium and the selection threshold T_RI.