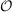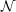9.6 Laplace-transformed SOS-RI-MP2 with 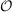(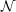⁴) scaling costs

The ricc2 module contains an implementation of SOS-MP2 which exploits the RI approximation and a Laplace transformation of the orbital energy denominators

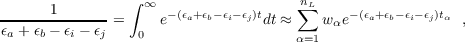(9.10)

to achieve an implementation with 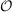(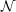⁴) scaling costs, opposed to the conventional 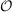(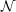⁵) scaling implementation. In particular for large molecules the Laplace-transformed implementation can reduce a lot the computational costs of SOS-MP2 calculations without loss in accuracy.

The Laplace-transformed implementation for SOS-MP2 calculations is activated with the input

where the parameter conv is a convergence threshold for the numerical integration in Eq. (9.10). A value of conv=5 means that the numerical integration will be converged to a root mean squared error of ≈ 10^-5 a.u.

Whether the conventional or the Laplace-transformed implementation will be more efficient depends firstly on the system size (the number of occupied orbitals) and secondly on the required accuracy (the number of grid points for the numerical integration in Eq. (9.10)) and can be understood and estimated from the following considerations:

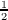• The computational costs for the most expensive step in (canonical) RI-MP2 energy calculations for large molecules requires O²V ²N _x floating point multiplications, where O and V are, respectively, the number occupied and virtual orbitals and N_x is the number of auxiliary functions for the RI approximation. For the LT-SOS-RI-MP2 implementation the most expensive step involves n_LOV N_x² floating point multiplications, where n_L is the number of grid points for the numerical integration. Thus, the ratio of the computational costs is approximately where for the last step N_x ≈ 3V (typical for valence TZ basis sets) has been assumed. Thus, the Laplace-transformed implementation will be faster than the conventional implementation if O > 6n_L.

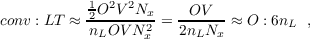
The number of grid points n_L depends on the requested accuracy and the spread of the orbital energy denominators in Eq. (9.10). The efficiency of Laplace-transformed SOS-RI-MP2 calculations can therefore (in difference to conventional RI-MP2 calculations) be enhanced significantly by a carefull choice of the thresholds, the basis set, and the orbitals included in the correlation treatment:

• The threshold conv for the numerical integration is by default set to the value of conv specified for the ground state energy in the data group $ricc2 (see Sec. 20.2.19), which is initialized using the threshold $denconv, which by default is set conservatively to the tight value of 10^-7.
  • For single point energy calculations conv in $laplace can savely be set to 4, which gives SOS-MP2 energies converged within ≈ 10^-4 a.u. with computational costs reduced by one third or more compared to calculations with the default settings for these thresholds.
  • For geometry optimizations with SOS-MP2 we recommend to set conv in $laplace to 5.
• The spread of the orbital energy denominators depends on the basis sets and the orbitals included in the correlation treatment. Most segmented contracted basis sets of triple-ζ or higher accuracy (as e.g. the TZVPP and QZVPP basis sets) lead to rather high lying “anti core” orbitals with orbital energies of 10 a.u. and more.
  • For the calculation of SOS-MP2 valence correlation energies it is recommended to exclude such orbitals from the correlation treatment (see input for $freeze in Sec. 20).
  • Alternatively one can use general contracted basis sets, as e.g. the correlation consistent cc-pVXZ basis sets. But note that general contracted basis sets increase the computational costs for the integral evaluation in the Hartree-Fock and, for gradient calculations, also the CPHF equations and related 4-index integral derivatives.
  • Also for the calculation of all-electron correlation energies with core-valence basis sets which include uncontracted steep functions it is recommended to check if extremely high-lying anti core orbitals can be excluded.

Note that for large molecules it is recommended to disable for geometry optimizations (or for gradient or property calculations in general) the preoptimization for the Z vector equations with the nozpreopt option in the $response data group (see Sec. 20.2.19).

Restrictions:

• It is presently not compatible with the calculation of the D₁ and D₂ diagnostics. The respective options will be ignored by program if the Laplace-transformed implementation is used.