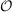 (
(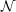 4)-scaling Laplace-transformed or
4)-scaling Laplace-transformed or 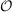 (
(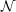 5)-scaling conventional RI implementation
is efficieint see Sec. 9.6.
5)-scaling conventional RI implementation
is efficieint see Sec. 9.6.
By introducing individual scaling factors for the same–spin and opposite–spin contributions to the correlation energy most second–order methods can be modified to achieve a (hopefully) better performance. SCS-MP2 has first been proposed by S. Grimme and SOS-MP2 by Y. Jung et al. (see below). The generalization of SCS and SOS to CC2 and ADC(2) for ground and excited states is described in [14]. It uses the same scaling factors as proposed for the original SCS- and SOS-MP2 approaches (see below). In the ricc2 program we have also implemented SCS and SOS variants of CIS(D) for excitation energies and of CIS(D∞) for excitation energies and gradients, which are derived from SCS-CC2 and SOS-CC2 in exactly the same manner as the unmodified methods can be derived as approximations to CC2 (see Sec. 10.2 and Ref. [159]). Please note, that the SCS-CIS(D) and SOS-CIS(D) approximations obtained in this way and implemented in ricc2 differ from the spin-component scaled SCS- and SOS-CIS(D) methods proposed by, respectively, S. Grimme and E. I. Ugorodina in [160] and Y. M. Rhee and M. Head–Gordon in [161].
A line with scaling factors has to be added in the $ricc2 data group:
cos denotes the scaling factor for the opposite–spin component, css the same–spin component.
As an abbreviation
scs
can be inserted in $ricc2. In this case, the SCS parameters cos=6/5 and css=1/3 proposed S.
Grimme (S. Grimme, J. Chem. Phys. 118 (2003) 9095.) are used. These parameters are also
recommended in [14] for the SCS variants of CC2, CIS(D), CIS(D∞), and ADC(2) for ground and
excited states.
Also, just
sos
can be used as a keyword, to switch to the SOS approach proposed by the Head-Gordon group for
MP2 with scaling factors of cos=1.3 and css=0.0 (Y., Jung, R.C. Lochan, A.D. Dutoi, and
M. Head-Gordon, J. Chem. Phys. 121 (2004) 9793.), which are also recommended for the SOS
variants of CC2, CIS(D), CIS(D∞), and ADC(2). The Laplace-transformed algorithm for the SOS
variants are activated by the additional data group $laplace:
For further details on the Laplace-transformed implementation and how one can estimated
whether the 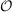 (
(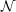 4)-scaling Laplace-transformed or
4)-scaling Laplace-transformed or 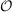 (
(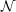 5)-scaling conventional RI implementation
is efficieint see Sec. 9.6.
5)-scaling conventional RI implementation
is efficieint see Sec. 9.6.
Since Version 6.6 the 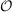 (
(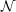 4)-scaling Laplace-transformed implementation is available for ground
and excited state gradients with CC2 and ADC(2).
4)-scaling Laplace-transformed implementation is available for ground
and excited state gradients with CC2 and ADC(2).