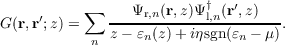
A method to systematically improve upon DFT estimates of single-particle excitation spectra, that is, ionization potentials and electron affinities, is the GW method. Its central object is the single-particle Green’s function G; its poles describe single-particle excitation energies and lifetimes. In particular, the poles up to the Fermi-level correspond to the primary vertical ionization energies. The GW-approach is based on an exact representation of G in terms of a power series of the screened Coulomb interaction W, which is called the Hedin equations. The GW-equations are obtained as an approximation to the Hedin-equations, in which the screened Coulomb interaction W is calculated neglecting so called vertex corrections. In this approximation the self–energy Σ, which connects the fully interacting Green’s function G to a reference non-interacting Green’s function G0, is given by Σ = GW.
This approach can be used to perturbatively calculate corrections to the Kohn–Sham spectrum. To this end, the Green’s function is expressed in a spectral representation as a sum of quasi particle states.
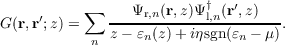 | (13.1) |
Under the approximation that the KS states are already a good approximation to these quasi–particle states Ψl,n the leading order correction can be calculated by solving the zeroth order quasi–particle equation:
 - V |n⟩
n n KS n xc](DOK214x.png) | (13.2) |
An approximation to the solution of this equation can be obtained by linearizing it:
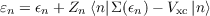 | (13.3) |
here, Zn is given by:
![[ ]-1
∂Σ(E )||
Zn = 1 - ⟨n |-∂E---|| |n⟩
E= ϵn](DOK216x.png) | (13.4) |
reducing the computational effort to a single iteration.
The self–energy Σ appearing in Eqn. (13.2) is calculated in the GW approximation from the KS Green’s function and screening. This is the so-called G0W0 approximation. The Self–energy splits in an energy independent exchange part Σx and a correlation part Σc(E) that does depend on energy. Their matrix elements are given by:
and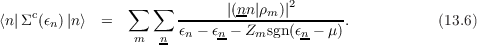
G0W0 is implemented in TURBOMOLE in the escf module supporting the following features.
The general recipe for a G0W0 calculation is as follows:
Ad 1) The def2-TZVPP basis seems to be the most useful, it comes for all tested systems within 0.1 eV of the def2-QZVP result with about half the number of basis functions. In the define session the calculation of the response function needs to be defined. In the final define menu select the ex menu and select the calculation of RPA singlet excitations, or urpa in case of open shell. Choose soghf to run a two-component calculation. Select "all all" to get all excitations. For systems and basis set having less than 4000 rpas excitations just set for all excitations. For large systems start to run G0W0 with ≈4000 rpas excitations. In subsequent runs add more excitations until a converged result is reached. escf will keep the converged roots, so not much time is lost using this restart approach.
Ad 2) If $gw is set in the control file the quasi particle energies will be evaluated according to equation 13.3. Additional options are described in the keywords section, Section 20.2.15.
Ad 3) Symmetry up to D2h is available for both closed shell (rpas) and open shell system (urpa) for GW. Moreover, the simplified methods xGW and sGW, which neglect contributions from excitation vectors are available for all point groups implemented in Turbomole. Two-component calculations can only be performed in C1.
Ad 4) In the escf run the response function is calculated which is needed to determine the screened coulomb interaction. At the end of this run the actual GW calculation is performed.
Possible source of errors: When dscf or ridft is repeated after escf the sing_a file may not be correct anymore, this may happen when degenerate levels are present. escf will however not recognize this and continue using the previously converged data in sing_a leading to nonsense values for Σc. Before running escf the old sing_a file has to be removed.