6.2 Exchange-Correlation Functionals Available

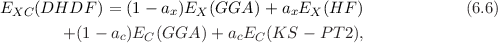
The following exchange-correlation functionals are available:

• LDAs: S-VWN, PWLDA
• GGAs: B-VWN, B-LYP, B-P, PBE
• MGGA: TPSS; SCAN; M06 (using XCFun)
• hybrid functionals: BH-LYP, B3-LYP, PBE0, TPSSh; M06-2X (using XCfun)
• double–hybrid functional: B2-PLYP (energy calculations only!)
• local hybrid functionals: Lh07t-SVWN, Lh07s-SVWN, Lh12ct-SsirPW92, Lh12ct-SsifPW92, Lh14t-calPBE

For EXX and LHF, see Chapter 19

The XCFun library (Arbitrary-Order Exchange-Correlation Functional Library) by Ulf Ekström and co-workers has been included [60] and some of the functionals implemented there can now be utilized. Among them are the empirically fitted MGGAs M06 and M06-2X from the Truhlar group [61]. XCFun functionals are available for energy, gradient, vib. frequencies and TDDFT excited state energy calculations - with and without RI approximation. For details and the license of XCFun please refer to its web site https://repo.ctcc.no/projects/xcfun/wiki See the next chapter for available functionals from XCFun.

In detail, the Turbomole own functional library consists of:

• The Slater–Dirac exchange functional only (S) [62,63].
• The 1980 correlation functional (functional V in the paper) of Vosko, Wilk, and Nusair only (VWN) [64].
• A combination of the Slater–Dirac exchange and Vosko, Wilk, and Nusair 1980 (functional V) correlation functionals (S-VWN) [62–64].
• The S-VWN functional with VWN functional III in the paper. This is the same functional form as available in the Gaussian program [62–64].
• A combination of the Slater–Dirac exchange and Perdew-Wang (1992) correlation functionals [62,63,65].
• A combination of the Slater–Dirac exchange and Becke’s 1988 exchange functionals (B88) [62,63,66].
• Lee, Yang, and Parr’s correlation functional (LYP) [67].
• The B-LYP exchange-correlation functional (B88 exchange and LYP correlation functionals) [62,63,66,67].
• The B-VWN exchange-correlation functional (B88 exchange and VWN (V) correlation functionals) [62–64,66].
• The B-P86 exchange-correlation functional (B88 exchange, VWN(V) and Perdew’s 1986 correlation functionals) [62–64,66,68].
• The Perdew, Burke, and Ernzerhof (PBE) exchange-correlation functional [62,63,65,69].
• The Tao, Perdew, Staroverov, and Scuseria functional (Slater–Dirac, TPSS exchange and Perdew-Wang (1992) and TPSS correlation functionals) [62,63, 65,70].
• The Strongly Constrained and Appropriately Normed (SCAN) meta-GGA functional [71].

For the SCAN functional, be advised that the convergence of the total energy and energy gradients with respect to the radial grid used to integrate the exchange-correlation energy and potential is slower than previous non-empirical functionals [72]. A radial grid size of 40 is typically needed to converge the total energy (dscfor ridft) to μH accuracy, while a radial grid size of 50 is typically needed to converge the energy gradients (grador rdgrad). Convergence with respect to the angular grids remains unchanged. The radial grid size can be set in the control file through the radsize keyword.

Additionally, for all four modules (dscf, grad, ridft, and rdgrad) the following hybrid functionals are available (a mixture of Hartree–Fock exchange with DFT exchange-correlation functionals):

• The BH-LYP exchange-correlation functional (Becke’s half-and-half exchange in a combination with the LYP correlation functional) [62,63,66,67,73].
• The B3-LYP exchange-correlation functional (Becke’s three-parameter functional) with the form,

  0.8S + 0.72B88 + 0.2HF + 0.19V WN(V ) + 0.81LY P

  (6.3)

  where HF denotes the Hartree-Fock exchange [62,63,66,67,74].
• The B3-LYP exchange-correlation functional with VWN functional V in the paper. This is the same functional form as available in the Gaussian program.
• The 1996 hybrid functional of Perdew, Burke, and Ernzerhof, with the form,

  0.75(S + PBE(X)) + 0.25HF + PW + PBE(C)

  (6.4)

  where PBE(X) and PBE(C) are the Perdew–Burke–Ernzerhof exchange and correlation functionals and PW is the Perdew–Wang correlation functional [62,63,65,69,75].
• The TPSSH exchange-correlation functional of Staroverov, Scuseria, Tao and Perdew with the form,

  0.9(S + TPSS(X)) + 0.1HF + PW + TPSS(C)

  (6.5)

  where HF denotes the Hartree–Fock exchange [62,63,65,70,76].

The Double-Hybrid Functional B2-PLYP can be used for single point energy calculations. Note that one has to run an MP2 calculation after the DFT step to get the correct B2-PLYP energy!

B2-PLYP is a so-called double-hybrid density functional (DHDF) [77] that uses in addition to a non-local exchange contribution (as in conventional hybrid-GGAs) also a non-local perturbation correction for the correlation part. In the following options/restrictions in the present version of this method:

• single point calculations only (computed with the DSCF/RIDFT and RIMP2/RICC2 modules).
• UKS treatment for open-shell cases.
• can be combined with resolution-of-identity approximation for the SCF step (RI-JK or RI-J option).
• can be combined with the dispersion correction (DFT-D method, s₆(B2-PLYP)=0.55).

The non-local perturbation correction to the correlation contribution is given by second-order perturbation theory. The idea is rooted in the ab initio Kohn-Sham perturbation theory (KS-PT2) by Görling and Levy [78,79]. The mixing is described by two empirical parameters a_x and a_c in the following manner:

(6.7)

The method is self-consistent only with respect to the first three terms in Eq. 6.6, i.e., first a SCF using a conventional hybrid-GGA is performed first. Based on these orbitals E_C(KS - PT2) is evaluated afterwards and added to the total energy.

For B2-PLYP, B88 exchange [66] and LYP correlation [67] are used with the parameters a_x = 0.53 and a_c = 0.27. Due to the relatively large Fock-exchange fraction, self-interaction error related problems are alleviated in B2-PLYP while unwanted side effects of this (reduced account of static correlation) are damped or eliminated by the PT2 term.

How to use B2-PLYP:

• during preparation of your input with DEFINE select b2-plyp in the DFT menu.
• carry out a DSCF run. Prepare and run a RI-MP2 calculation with either RIMP2 or RICC2 program modules.
• the RI-MP2 program directly prints the B2PLYP energy if this functional has been chosen before

Or use the b2plypprep script to setup up the calculation.

• define coord and basis set
• (optional: switch on ri or rijk and define jbasis or jkbasis)
• run b2plypprep
• run DSCF (or RIDFT) and RICC2

Local hybrid functionals [80] feature an admixture of the exact-exchange energy density to a (semi-)local exchange energy density in real space managed by a local mixing function (LMF). They can therefore be viewed as a more flexible generalization of global hybrid functionals.

So far, local hybrid functionals are available in the modules ridft, [81] grad, rdgrad, [82] and escf. [83] For the calculation of non-standard exact-exchange integrals, a semi-numerical integration scheme is used. The usual DFT grids are employed for this task and small grids are thus recommended if possible. To accelerate local hybrid calculations, the analytical integrals for exact exchange are screened using the overlap and the density matrix (see S- and P-junctions Sec. 20.2.7 for details). In escf-calculations, a larger amount of main memory is required for the semi-numerical integration. Therefore, additional main memory of approximately 0.0004 ⋅N_BF ² MB should be provided (for each CPU).

The following local hybrid functionals are available so far:

• Lh07t-SVWN: [84] Slater-Dirac exchange [62,63] and VWN [64] with t-LMF (prefactor of 0.48)
• Lh07s-SVWN: [85] Slater-Dirac exchange [62,63] and VWN [64] with s-LMF
• Lh12ct-SsirPW92: [86] Slater-Dirac exchange [62,63] and self-correlation-reduced PW92 correlation with common t-LMF (prefactor of 0.646)
• Lh12ct-SsifPW92: [86] Slater-Dirac exchange [62,63] and self-correlation-free PW92 correlation with common t-LMF (prefactor of 0.709)
• Lh14t-calPBE: [87] PBE exchange and correlation [62,63,65,69] with t-LMF (prefactor pf 0.5) and pig1 calibration [88]

D3 parameters for these local hybrid functionals have been implemented. [89] Note that Lh14t-calPBE is not available in grad, and rdgrad and requires larger numerical grids in escf-calculations.

For gradient calculations it is strongly recommended to use the weight derivatives keyword in the $dft data group to avert numerical inaccuracies.

6.2.1 Exchange-Correlation Functionals from XCFun library

The XCFun library is taken from: https://repo.ctcc.no/projects/xcfun/wiki

The current TURBOMOLE version uses XCFun 1.99 and enables the usage of individual mixtures of the available exchange and correlation functionals.

To trigger the usage of XCFun functionals, use the keyword xcfun in the $dft section:

In addition to the name of the functional, it is necessary to tell TURBOMOLE whether the used functional is of GGA or MGGA type. Pure LDA functionals are currently not supported.

Available settings are:

• functional xcfun set-gga – sets a GGA functional
• functional xcfun set-mgga – sets a meta-GGA functional
• functional xcfun set-hybrid 0.2 – defines a hybrid functional with a portion of 0.2 of Hartree-Fock exchange

Add the switch for either GGA or meta-GGA but not both in the same input!

List of available XCFun functionals (copied from XCFun documentation), in arbitrary order:

Some common functionals are pre-defined in XCFun and their individual parts do not have to be set manually. Those aliases can be directly used as names with a following factor of 1.0:

blyp, pbe, bp86, kt1, kt2, kt3, pbe0, b3lyp, m06, m06-2x, m06L, b3lyp-g, b3p86, b97, b97d, olyp and some more.

Note that if the functional needs a portion of HF exchange, this has to be added manually in the control file using functional xcfun set-hybrid <number>

Example for B3-LYP using VWN3 instead of VWN5:

The functionals described in this section can be used for ground state energies, gradients and frequency calculations as well as TDDFT spectra. TDDFT analytic gradients are not yet supported, please use the TURBOMOLE own functionals instead.

Notes about DFT-D3, gCP and functionals using those corrections

For details about the options of DFT-D3 please see section 6.5.

In the original TURBOMOLE implementation of the B97-D functional only energy and gradient calculations are possible due to missing higher derivatives of the functional itself. Using the XCFun version of B97-D, analytic 2nd derivatives using aoforceand TDDFT excited state energies are possible. The names in the $dft section are b97-d for the TURBOMOLE own version and b97d for the XCFun version. However, the total energies of those two flavours are slightly different due to the fact that the parameters used are either the originally published ones (TURBOMOLE) or re-computed (XCFun). For properties like geometries and frequencies the differences are negligible, but one should not mix the total energies.

The PBEh-3c functional needs, besides the functional name pbeh-3c also DFT-D3 dispersion correction including the three-body term and geometrical counterpoise correction method called gCP. For details see: Stefan Grimme, University Bonn. In order to get the full version of PBEh-3c, your control file has to include:

Note: gcp is automatically added if pbeh-3c functional is used, but the D3 part has to be switched on manually by adding $disp3 as given above.

To use HF-3c ( R. Sure, S. Grimme, J. Comput. Chem. 2013, 34, 1672–1685), an input without DFT functional (and without $dft keyword) but with DFT-D3 correction is required. Calculations with and without RI are possible to perform, but due to the very small basis set non-RI calculations are usually as efficient as those with RI. Note that it is important to use the ’Minix’ basis set and to select hf-3c as functional name for DFT-D3:

The gCP correction (H. Kruse, S. Grimme, J. Chem. Phys. 2012, 136, 154101) will by default be added to the DFT-D3 correction term if pbeh-3c or hf-3c is selected.