17.3 Frozen Density Embedding calculations

17.3.1 Background Theory

In the subsystem formulation of the density-functional theory a large system is decomposed into several constituting fragments that are treated individually. This approach offers the advantage of focusing the attention and computational cost on a limited portion of the whole system while including all the remaining enviromental effects through an effective embedding potential. Here we refer in particular to the (fully-variational) Frozen Density Embedding (FDE) [196] with the Kohn-Sham Constrained Electron Density (KSCED) equations [197,198].

In the FDE/KSCED method the embedding potential required by an embedded subsystem with density ρ_A to account for the presence of another (frozen) subsystem with density ρ_B is:

(17.1)

where v_ext^B(r) and v_J[ρ_B](r) are the electrostatic potentials generated by the nuclei and electron density of the subsystem B, respectively, and

(17.2)

(17.3)

are the non-additive non-interacting kinetic energy and exchange-correlation energy functionals, respectively. In the expressions above T_s[ρ] is the (unknown) non-interacting kinetic energy density functional and E_xc[ρ] is the exchange-correlation energy functional. Note that, while the first two terms in Eq. (17.1) refer to classical electrostatics (and could be described by e.g. external point-charges), the last two terms are related to quantum-mechanical effects.

Using freeze-and-thaw [199] cycles, the role of the frozen and the embedded subsystem is iteratively exchanged, till convergence. If expressions (17.2) and (17.3) are computed exactly, then the density ρ_A + ρ_B will coincide with the exact density of the total system.

Because the FDE/KSCED was originally developed in the Kohn-Sham framework, using standard GGA approximations for E_xc[ρ], the non-additive exchange-correlation potential (δE_xc^nadd∕δρ_A(r)) can be computed exactly as a functional of the density, leaving the expression of the non-additive kinetic energy term as the only approximation (with respect the corresponding GGA calculation of the total system), because the exact explicit density dependence of T_s from the density is not known. Using GGA approximations for the kinetic energy functional (T_s ≈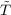_s^GGA) we have:

(17.4)

and

(17.5)

where ṽ_T^GGA(r) = δ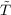_s^GGA∕δρ(r).

The FDE total energy of total system is:

Using the Generalized Kohn-Sham (GKS) theory, also hybrid exchange-correlation functionals can be used in embedding calculations. To obtain a practical computational method, the obtained embedding potential must be approximated by a local expression as shown in Ref. [200]. This corresponds to performing for each subsystem hybrid calculations including the interaction with other subsystems through an embedding potential derived at a semilocal level of theory. When orbital dependent exchange-correlation functionals (e.g. hybrid functional and LHF) are considered within the FDE method, the embedding potential includes a non-additive exchange-correlation term of the form

(17.7)

where Φ^A+B[ρ_A + ρ_B] denotes the Slater determinant which yields the total density ρ_A + ρ_B. Since such a determinant is not easily available, the non-additive exchange-correlation contribution cannot be determined directly and the non-additive exchange-correlation term can be approximated as [201]

(17.8)

17.3.2 Frozen Density Embedding calculations using the FDE script

The shell script FDE controls and executes automatically FDE calculations. The script FDE prepares the input files (running define), runs the calculations (only dscf is supported in the present versiob), and combines the results (running fdetools). Because the FDE equations are coupled sets of one-electron equations (one for each subsystem), full relaxation of the electron densities of both subsystems is obtained by using a freeze-and-thaw [199] procedure until convergence.
The converged FDE calculations are store in the subdirectories STEPN/SUBSYSTEM_A and STEPN/SUBSYSTEM_B, where N is the number of the FDE iteration. The subdirectory ISOLATED_SUBSYSTEM_A and ISOLATED_SUBSYSTEM_B contain instead the calculations for isolated subsystems (see also Section 17.3.3).

Current functionalities and limitations of FDE are:

• only C₁ point group;
• only for closed-shell systems that consist of two closed-shell subsystems (e.g. weakly interacting closed-shell dimers);
• only total and binding energy calculations (no gradients);
• serial and OMP dscf runs (no MPI);
• monomolecular and supermolecular basis set approach;
• LDA/GGA kinetic energy functionals (for weakly interacting systems);
• full or pure electrostatic embedding;
• LDA/GGA, hybrid or orbital-dependent exchange-correlation potentials;
• multilevel FDE calculation;
• energy-decompostion;
• FDE calculation with subsystem B taken frozen.

In order to perform a FDE calculation, the files coord and control for the total system are necessary to take informations on atomic coordinates and basis sets. The input file for the total system can be generated, as usual, with define but no calculation on the total system is required. $denconv 1.d-7 option should be defined in file control in order to better converge the embedded densities and better describe the dipole moment.

Given a closed-shell supramolecular system with a GGA/LDA exchange-correlation functional, the command

invokes an iterative resolution of the KSCED equations with revAPBEk [202,203] as approximation of the non-additive kinetic potential (see Eq. 17.5) in the monomolecular basis set approach. The two subsystems are defined via an integer m = 3 in the example above which identifies the first atom of the subsystem B in the file coord of the supramolecular system with n atoms, where the atoms 1…m - 1 belong to the subsystem A while the atoms m…n to the B one. Thus the file coord must contains first all the atoms of the system A and then all the atoms of the system B.

As an example we report here the FDE -p 3 output for the HF dimer:

The final energies are stored in the file fde_energy. The directory STEPN/ENERGY_SYSTEM contains the total system with density ρ_A + ρ_B; this directory can (only) be used for density analysis.

17.3.3 Options

All the options for the FDE can be specified as commandlines, and are described below. The options can be also be specified in file fde.input, which is read by the FDE script. If fde.input is not present it is created by the FDE script. Command lines options overwrites options found in the fde.input file.

Subsystem definition

The flag -p integer is required or it must be present in the fde.input file.

Equivalent command: --pos-cut integer

fde.input option: pos-cut= integer

Kinetic-energy functionals

In order to use different GGA approximations of the non-additive kinetic potential, the flag -k string must be used. Here string is the acronym used to identify a given GGA kinetic energy approximation, that can be selected among the following functionals:

• string=revapbek: generalized gradient approximation with a PBE-like enhancement factor, obtained using the asymptotic expansions of the semiclassical neutral atom as reference [202,203] (revAPBEk). This is the default choice;
• string=lc94: Perdew-Wang (PW91) exchange functional reparametrized for kinetic energy by Lembarki and Chermette [204] (LC94);
• string=t-f: gradient expansion truncated at the zeroth order (GEA0), corresponding to the Thomas-Fermi functional.

For example, the command

approximates the non-additive kinetic contribution to the embedding potential through the functional derivative of LC94 kinetic energy functional.

A pure electrostatic embedding can be also performed with FDE script, where the embedding potential required by a subsystem A to account for the presence of the B one will be merely:

(17.9)

with v_ext^B(r) and v_J[ρ_B](r) the electrostatic potentials generated respectively by the nuclei and electron density of the subsystem B. To perform an electrostatic embedding calculation use

and can be performed for both Kohn-Sham (only for LDA/GGA exchange-correlation functionals) and Hartree-Fock methods.

The electrostatic embedding is implemented only for testing purpose. It resembles an electrostatic embedding with external point-charges and/or point-dipoles, but it is “exact” as it is based on the whole densities (i.e. it considers all multipole moments of the density and the polarizabilies at all orders).

Equivalent command: --kin string

fde.input option: kin= string

FDE charged subsystems

FDE can perform calculations for charged closed-shell systems whose charge is localized on one or both subsystems. To localize the charge on a given subsystem, --chargeA= integer must be used for the subsystem A and --chargeB= integer for the B one. Here integer denotes the charge added to the neutral subsystem. For example, the command

performs a FDE calculation for a negative charged closed shell system (for example Zn( H₂O)₂²⁺) whose subsystem B has charge 2. Note that in this case the starting control file must have a charge +2.

fde.input option: chargeA= integer , chargeB= integer

FDE with subsystem B taken frozen

FDE can perform embedding calculations where the subsystem B is taken frozen, i.e. without scf calculation on it using an embedding potential. Therefore only one step will be performed if the flag --frozen will be used

The frozen embedding calculation is store in the subdirectory STEP1/SUBSYSTEM_A. The control file is modified with the following keywords:

The program dscf will read the submatrices fde_ZJ.mat and fde_KXC.mat and add them to the Hamiltonian.

fde.input option: frozen=1

Parallel calculations

If PARA_ARCH=SMP and OMP calculation will be performed. The flag -nth nthreads can be used to specify the number of threads. For example, with the following command

will use 4 threads.

Equivalent command: --nthreads integer

fde.input option: nthreads= integer

Monomolecular and supermolecular basis set approach

The ρ_A and ρ_B densities can be expanded using the supermolecular or monomolecular basis set. In a supermolecular basis set expansion the basis functions {χ} of both subsystems are employed to expand the subsystem electron densities. In a monomolecular basis set expansion, instead, only basis functions {χ^ℓ} centered on the atoms in the ℓ-th subsystem are used to expand the corresponding density.

Both monomolecular and supermolecular basis set expansion of the electron densities are implemented in FDE: with the flag -m a monomolecular expansion is performed, while for a supermolecular one -s is used. In the absence of both flags a monomolecular expansion is performed by default.

For an accurate calculation of binding-energies of weakly interacting molecular systems a supermolecular basis set is required (to avoid the basis-set superposition error). Otherwise a very large monomolecular basis set is necessary.

NOTE: The FDE script supports only basis-set in the TURBOMOLE library.

Equivalent command: --mono or --super

fde.input option: method=mono or method=super

Convergence of the freeze-and-thaw cycles

The script FDE runs a self-consistent calculation when a convergence criterion is fulfilled. The convergence criterion is the change in the total dipole moment. This is a tight convergence criterion, as the dipole moment is highly sensitive to small changes in electron density. The convergence parameter ε^j for the j-th step in the freeze-and-thaw procedure is computed by means the following expression

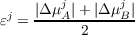(17.10)

where

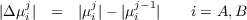
The maximum number of freeze-and-thaw cycles can be specified by --max-iter= integer, and the default value is 20.

In order to make easy the convergence of the iterative solution of the KSCED coupled equations, a damping factor η must be used for the matrix elements of the embedding potential v_embij as perturbation to a given subsystem

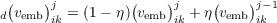(17.11)

for the j-th iteration. Here _dv_embik^j is the matrix element effectively used in the j-th iteration after the damping. In FDE the starting value of η can be changed using --start-damp= real (default value is 0.45) where real is a decimal number. The damping parameter can also dynamically change at each iterative step (according to the convergence process) of a quantity set by --step-damp= real (default value is 0.10). The minimum value set by --max-damp= real (default value is 0.90).

fde.input options:
  epsilon= real
  max-iter= integer
  start-damp= real
  max-damp= real
  step-damp= real

Embedding energy error

The embedding error in the total energy is computed as

(17.12)

where E^DFT is the DFT total energy of total system with density ρ(r). In order to compute ΔE as well as its components, the flag --err-energy must be used. This flag will required also the DFT calculation on the total system. In this case the converged SCF output file must be named output.dscf.

An example of session output for the computation of embedding energy and energy error decomposition, when --err-energy flag is present, is the following:

where the FDE energy (E^FDE), the FDE binding energy, the embedding energy error (ΔE) and the error energy decomposition in its coulomb, nuclear, exchange-correlation and kinetic contributions are reported. This output is present at each FDE iteration.

fde.input option: err-energy=1

Restarting

The script FDE checks in the current directory for previous FDE calculations. If these are present, then the FDE calculation will be restarted from the last iteration found. The directories ISOLATED_SUBSYSTEM_A and ISOLATED_SUBSYSTEM_B will be overwritten by the converged calculations from previous run. The energy and the orbital from the isolated systems are saved in the current directory in the files: isolated_energy.ks, mos_A.ks and mos_B.ks.

Note that a restart is possible only if the same subsystem definition and the same basis set are used (e.g. the same -p flag and the -s or -m flag). Other flags, e.g. kinetic and xc-functionals and convergence paramters, can be instead modified.

As all the options are saved in the fde.input file, to restart a FDE calculation the FDE script can be inkoved without any parameters.

To force a calculation from scratch use:

17.3.4 FDE with hybrid and orbital-dependent functionals

In order to use local approximations (17.1) and (17.8) with FDE, the flag -f string must be add to the options of the script. Here string denotes the local/semilocal approximation to hybrid or orbital-dependent exchange-correlation potentials in v_emb(r). All LDA/GGA functionals in TURBOMOLE can be considered as approximations.

For example, the command

can be used to approximate bh-lyp or b3-lyp hybrid non-additive potentials, while the command

approximates the pbe0 hybrid non-additive potentials. Other combinations of functionals are not recommended (meta-GGA are not supported).

Finally, also calculations with the Local Hartree-Fock (LHF) potential can be performed. In this case the command

can be used to approximate the LHF non-additive potential [201].

Equivalent command: --func string

fde.input option: func= string