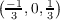 , k2 ∈
, k2 ∈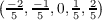 , and k2 ∈
, and k2 ∈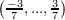 The
kpoints and $pointvalper groups are:
The
kpoints and $pointvalper groups are:
In periodic systems too diffuse basis functions result in near-singularity of the overlap matrix. Therefore, it is recommended that the exponents of the Gaussian basis sets used for periodic calculations are not smaller than 0.01. Optimally, the exponents should be larger than 0.1. The easiest way to achieve this is to remove the small exponent basis functions from the basis sets. Optionally, basis sets optimized for periodic calculations can be used, such as the ones in Ref. [113]. They are available in the TURBOMOLE basis sets library as pob-TZVP.
Calculations using riper require the control file and starting orbitals generated using define. DFT method needs to be specified in the $dft data group. All LDA, GGA and meta-GGA exchange-correlation functionals including interface to the XCFun library (see Sec. 6.2) are supported. Moreover, auxiliary basis sets defined in the data group $jbas are required. For periodic calculations additional keywords specifying the system periodicity and number of k points (if used) have to be added manually to the control file. Optionally, the $riper group containing control options specific to riper (including the LMIDF keywords) can be added. The input preparation steps are summarized below. More detailed information about riper keywords are provided in Sec. 20.2.11.
Specification of cell parameters using the $cell keyword depends on the periodicity of a system:
Alternatively, lattice vectors can be provided using the $lattice keyword:
Example 1: 1D periodic system with a unit cell |a| = 5 bohr:
The same input using the $lattice keyword:
Example 2: 2D periodic system with a unit cell |a| = 5 and |b| = 8 bohr, the angle between a and b of 60∘:
Similar input using the $lattice keyword:
Example 3: 3D periodic system with a triclinic unit cell |a| = 5, |b| = 8 and |c| = 6 bohr, the angle between b and c of 70∘, between a and c of 60∘, and between a and b of 90∘:
Similar input using the $lattice keyword:
The following examples illustrate the additions to the control file required for calculations using the riper module.
Example 1: In this example a 3D periodic system is defined ($periodic 3). The unit cell is specified using the $cell keyword, with lengths and angles given in atomic units and degrees, respectively. A uniform grid of 27 (3 ⋅ 3 ⋅ 3) k points for numerical integration over the BZ is specified using the keyword $kpoints. The section $riper (see Sec. 20.2.11) is added with the keyword lenonly set to on. It forces riper to skip the calculation of energy gradients (by default both energy and gradients are calculated in one run). In addition, Gaussian smearing is switched on by providing sigma 0.01 (see Sec. 7.2.4).
The same input using the $lattice keyword:
Example 2: In this example a 2D periodic system is defined ($periodic 2). The unit cell is specified using the $cell keyword, with lengths and angles given in Å and degrees, respectively. A uniform grid of 9 (3 ⋅ 3) k-points for numerical integration over the BZ is defined using the keyword $kpoints. The section $riper (see Sec. 20.2.11) is added with the keyword lmaxmom 30. This changes the maximum order of multipole expansions used in CFMM to 30 (default value is 20).
The same input using the $lattice keyword:
Example 3: In this example a 1D periodic system is defined ($periodic 1). The dimension of the periodic direction in atomic units is specified using the $cell keyword. A one dimensional grid of 3 k-points for numerical integration over the BZ is defined using the keyword $kpoints.
The same input using the $lattice keyword:
Example 4: In this example a molecular system is defined (default if no $periodic is specified). The section $riper (see Sec. 20.2.11) is added with the keyword lpcg on, which activates the low-memory modification of the RI approximation for calculations on very large molecular systems.
By default riper calculates single point energy and gradient in one run. For this, simply invoke riper as
For energy calculation only add lenonly on to the $riper section in the control file, i.e.,
The parallel OpenMP version of riper can be invoked ad described in Sec. 3.2.2.
jobex will automatically use riper when the keyword $periodic is present in the control file. Alternatively, the use of riper can be forced by specifying -riper argument of jobex, i.e., invoking
Note, that at present only structure optimization using Cartesian coordinates is possible when using periodic boundary conditions. Using internal coordinates for periodic systems will lead to convergence problems in structure optimizations.
Simultaneous optimization of atomic positions and cell parameters or lattice vectors can be performed by specifying the keyword $optcell in the control file and then invoking the jobex script as described in 7.3.5.
The calculation of energy first derivatives with respect to lattice vectors usually requires higher accuracy than nuclear gradients. Therefore, in case of convergence issues it is recommended to decrease the SCF convergence threshold to at least 1.0 × 10-7 by specifying $scfconv 7. In addition, convergence can often be improved by including weight derivatives by adding the option weight derivatives in the $dft data group.
Band structure plots show the values of band (orbital) energies for values of k along lines connecting symmetry points. In riper these lines can be specified by providing their start and end points as well as the number of k points along the line within the $kpoints section. They will be calculated at the end of SCF procedure and written to the file bands.xyz.
In the following example band energies are calculated along four lines, as specified by the keyword kptlines 4. Each line definition starts in a new line with the keyword recipr, followed by three real numbers defining the start point of the line and three real numbers defining its end point. Finally, the number of k points along the line is given as an integer number. Thus, the first line starts at the point (0.500 0.500 0.500), ends at (0.000 0.000 0.000) and contains 40 k points.
Each line of the resulting bands.xyz file contains five real numbers: the coordinates k1, k2 and k3 of the k point, its length |k| and the corresponding band energy ϵnk.
Calculation of data on grids for molecular and periodic systems using riper requires the keyword $pointvalper in the control file. The values are calculated on a 3D grid and written to appropriate output files. These files can be generated either running a single point energy riper calculation or invoking
provided that converged orbitals and occupation numbers from previous calculation are present in the files RIPER.BANDS and RIPER.BANDS.OCCUPATIONS, respectively.
The format of the output files can be specified using the keyword fmt= following $pointvalper in the same line. Supported formats are:
(default) The generated data is written to binary files that can be read by gOpenMol and other external visualization programs. This format uses orthogonal grids. Therefore, for non-orthogonal unit cells grid data is generated for a rectangular box that contains the supercell (unit cell and its periodic images). By default, the values at grid points outside of the supercell are set to zero. For strongly non-orthogonal systems this may lead to large files. The option full switches off the zeroing of values on grid points outside the supercell.
Gaussian cube format. Can be imported by several external visualization programs.
Coordinates of grid points and calculated values are stored in a text file. Each line contains Cartesian grid point coordinates and the corresponding value.
Values and grid data is output to binary files. First 8 (integer) records are: 1-2) rank value and descriptor, 3-8) number of grid points and number of periodic unit cell images in each periodic direction, 9...) Cartesian coordinates and the corresponding value repeated for all grid points.
Output files in cub format contain information about atomic coordinates. For other formats additional coord.xyz file containing atomic coordinates is generated.
The following options can be used along with the keyword $pointvalper:
Number of unit cell images n1, n2 and n3 in the periodic directions a, b and c,
respectively, for which plot data is generated.
Number of grid points n1, n2 and n3 along each periodic direction. If not specified,
value 100 is used for each n.
Specifies the distance real in bohr around the system for which plot grid is generated
in aperiodic directions. Default value is 5 bohr.
Number of grid points stored in one octree box during density calculations. Default
value is 50. For very large systems or high resolution it may be necessary to increase
this parameter to avoid memory allocation problems.
Only valid for plt output format. Switches off zeroing of values on grid points outside
the supercell.
Plots of electron density require option dens in the $pointvalper data group
The values of the total density and, in case of UHF calculations also the spin density are written to files td.fmt and sd.fmt, respectively, where fmt is the selected format.
Plot files for visualization of molecular orbitals can be generated by setting orbs n in the $pointvalper data group, where n is the number of orbitals to plot. The way to specify the orbitals is best explained by some examples:
example 1: An open shell system is considered. Number of k points along the reciprocal lattice
vectors b1, b2 and b3 is 3, 5, and 7, respectively. Possible k point components kj calculated from
equation 7.16 are therefore k1 ∈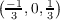 , k2 ∈
, k2 ∈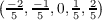 , and k2 ∈
, and k2 ∈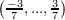 The
kpoints and $pointvalper groups are:
The
kpoints and $pointvalper groups are:
Here, two orbitals will be plotted. They are defined in two lines following the orb 2 option. Each
line starts with k followed by three numbers that specify which of possible components kj
are used. In this example k point components for the first orbital are 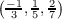 . For
the second one k = (0,0,0), i.e., this orbital is at the Γ-point. Subsequently, type and
number of the orbitals are defined (orbitals at each k-point are ordered by increasing
energy). Here the first one is a 1 - the lowest α orbital. Similarly, b 3 denotes the third
lowest energy β orbital. Finally it is specified if real (r) or imaginary (i) contribution is
plotted.
. For
the second one k = (0,0,0), i.e., this orbital is at the Γ-point. Subsequently, type and
number of the orbitals are defined (orbitals at each k-point are ordered by increasing
energy). Here the first one is a 1 - the lowest α orbital. Similarly, b 3 denotes the third
lowest energy β orbital. Finally it is specified if real (r) or imaginary (i) contribution is
plotted.
example 2: In this example a closed shell system with 3, 2 and 4 k points in each direction is given:
Possible k point components from equation 7.16 are k1 ∈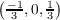 , k2 ∈
, k2 ∈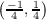 and
k2 ∈
and
k2 ∈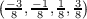 . In analogy to the previous example, the first and the second generated data
files will contain, respectively, the real and the imaginary part of the lowest energy orbital at k
point
. In analogy to the previous example, the first and the second generated data
files will contain, respectively, the real and the imaginary part of the lowest energy orbital at k
point 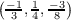 . Third file contains the real part of the second lowest energy orbital at the
Γ-point. Orbitals at this point are defined by using ’special’ 0 0 0 component indices, as it is not
included in the grid.
. Third file contains the real part of the second lowest energy orbital at the
Γ-point. Orbitals at this point are defined by using ’special’ 0 0 0 component indices, as it is not
included in the grid.
example 3 In this example an input for a Γ-point calculation is shown:
Here k 1 1 1 is the only valid option. For Γ-point calculation orbitals are real, thus there is no possibility to plot the imaginary part. In this case the fifth lowest energy orbitals with spin components α and β are plotted.
A simulated density of states (DOS) is calculated by broadening the discrete energy levels with Gaussians and superimposing them. The output files (dos for RKS calculations, and dos_a+b, dos_a-b, dos_alpha, dos_beta in case of UKS) contain energies (first column) and corresponding total DOS (second column) as well as s-, p-, ... contributions (following columns). The calculation is controlled by the keyword $dosper:
The parameters in example above have the following meaning:
the width of each Gaussian, default value is 0.01 a.u.
lower/upper bounds for energy in DOS calculation
scaling factor for DOS (total and s-, p-, ... contributions)
resolution (number of points)
All parameters are optional, default values are usually sufficient to generate a satisfactory plot. DOS files can be generated either running a single point energy riper calculation or using -proper option
provided that converged orbitals and occupation numbers from previous calculation are present in the files RIPER.BANDS and RIPER.BANDS.OCCUPATIONS, respectively.